- Diese Veranstaltung hat bereits stattgefunden.
Digits and Sounds: Konzert
5. Juli 2024 // 19:00 -20:30

Das Konzert umfasst vier Stücke aus verschiedenen Epochen – zwei davon instrumental, die beiden anderen elektronisch. Mit Çoǧluotobüsişletmesi aus dem Jahr 1979, einem Stück, das Barlows Ruhm als führender Computerkomponist begründete und als eines der schwierigsten für Klavier geschriebenen Stücke gilt, sowie 3C2=[ħ] Chronometry aus dem Jahr 2017 repräsentiert das Konzert 38 Jahre Barlows kreativen Lebens, in denen er u.a. wichtige Beiträge zu algorithmischer und multimedialer Komposition, Konzeptualismus und Spektralismus leistete. Seine Stück Pinball Play, in dem ein musikalischer Ball von den Noten der Bohlen-Pierce-Skala abprallt, oder Approximating Pi, das auf musikalischer Ebene hält, was der Titel verspricht, zeichnen sich einerseits durch einen strengen Sinn für Kontrolle und andererseits durch Verspieltheit, Humor und einen Hang zu Zweideutigkeit und Illusion aus. Die Dinge sind nicht das, was sie zu sein scheinen, oder sie sind mehrere Dinge auf einmal.
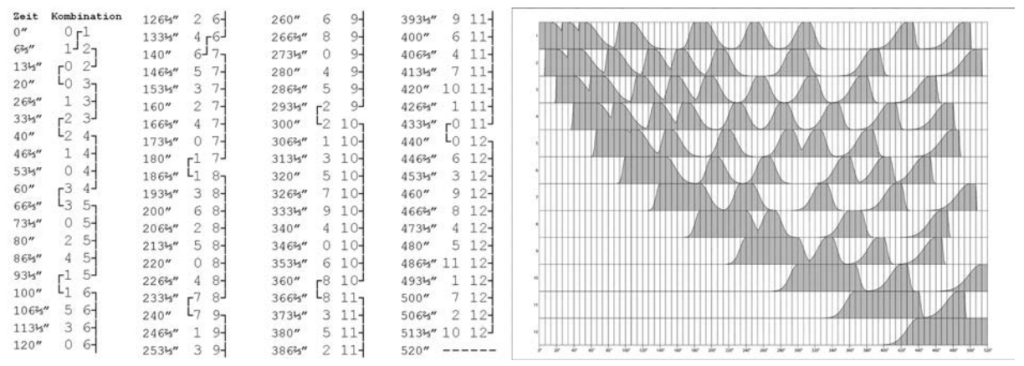 Die Tabelle links zeigt 78 gleich lange Zeitperioden, die jeweils zwei am Maximalpegel simultan erklingende Tonspuren kombinieren, wobei „0“ eine nicht existente und „1“ bis „12“ zwölf real existente Tonspuren bezeichnen. Jede Zeitperiode hat mit der darauf folgenden eine spezifische, durch eine Klammer angezeigte Tonspur gemeinsam. 13C2=[♄] ist ein perkussives Stück, in dem zwölf „Instrumente“ in zwölf Tonspuren ein Perpetuum Mobile spielen, und zwar in insgesamt 48 Metren, die jeweils ein bis zwölf Pulse enthalten, neun pro Sekunde. Jede Spur beginnt in einem Metrum mit einer Anzahl von Pulsen die der Spurnummer gleicht. Jedes Metrum (außer jenem mit nur einem Puls) entspricht einer einmaligen Permutation von Gruppen von zwei und/oder drei Pulsen, z.B. in den drei 7-Puls-Metren 2+2+3, 2+3+2 and 3+2+2. Die Metren mit einer Länge von 12 Pulsen sind zwölf an der Zahl. Bei 6’13⅓” fangen die Metren an – Spur für Spur – in der Länge zu wachsen, und zwar bis 7’20”, wo alle zwölf Spuren gleich lange, doch unterschiedliche, synchronisierte 12-Puls-Metren enthalten. Die „Instrumente“ um die es sich hier handelt, sind synthetische klangfarbliche Interpolierungen zwischen Sinus- (bei Spur 1) und Sägezahnschwingungen (Spur 12). Dazu – inspiriert von der Arbeit von J. M. Grey et al. (1978) – werden die Spektren durch ein hinzugefügtes steigendes formantartiges Gebilde („spectral centroid“) von Spur zu Spur klangfarblich heller unter Zuspitzung der Anschlagszeit. Die Grundtonhöhen dieser Spektren – von 110 bis 208 Hz (A bis gis) chromatisch steigend – entsprechen der von mir errechneten metrischen Priorität der Pulse.
Die Tabelle links zeigt 78 gleich lange Zeitperioden, die jeweils zwei am Maximalpegel simultan erklingende Tonspuren kombinieren, wobei „0“ eine nicht existente und „1“ bis „12“ zwölf real existente Tonspuren bezeichnen. Jede Zeitperiode hat mit der darauf folgenden eine spezifische, durch eine Klammer angezeigte Tonspur gemeinsam. 13C2=[♄] ist ein perkussives Stück, in dem zwölf „Instrumente“ in zwölf Tonspuren ein Perpetuum Mobile spielen, und zwar in insgesamt 48 Metren, die jeweils ein bis zwölf Pulse enthalten, neun pro Sekunde. Jede Spur beginnt in einem Metrum mit einer Anzahl von Pulsen die der Spurnummer gleicht. Jedes Metrum (außer jenem mit nur einem Puls) entspricht einer einmaligen Permutation von Gruppen von zwei und/oder drei Pulsen, z.B. in den drei 7-Puls-Metren 2+2+3, 2+3+2 and 3+2+2. Die Metren mit einer Länge von 12 Pulsen sind zwölf an der Zahl. Bei 6’13⅓” fangen die Metren an – Spur für Spur – in der Länge zu wachsen, und zwar bis 7’20”, wo alle zwölf Spuren gleich lange, doch unterschiedliche, synchronisierte 12-Puls-Metren enthalten. Die „Instrumente“ um die es sich hier handelt, sind synthetische klangfarbliche Interpolierungen zwischen Sinus- (bei Spur 1) und Sägezahnschwingungen (Spur 12). Dazu – inspiriert von der Arbeit von J. M. Grey et al. (1978) – werden die Spektren durch ein hinzugefügtes steigendes formantartiges Gebilde („spectral centroid“) von Spur zu Spur klangfarblich heller unter Zuspitzung der Anschlagszeit. Die Grundtonhöhen dieser Spektren – von 110 bis 208 Hz (A bis gis) chromatisch steigend – entsprechen der von mir errechneten metrischen Priorität der Pulse.Daan Vandewalle ist ein international gefeierter Interpret von Klaviermusik des 20. und 21. Jahrhunderts. Sein Repertoire umfasst Hunderte von Stücken, darunter Gesamtausgaben der meisten bekannten Komponisten des 20. Jahrhunderts wie Ives, Messiaen und Schönberg sowie zahlreiche Uraufführungen, die aus der intensiven Zusammenarbeit mit zeitgenössischen Komponisten hervorgegangen sind. Er ist an den unterschiedlichsten Orten aufgetreten, von kleinen Clubs in der Underground- und experimentellen Musikszene bis hin zu etablierten Veranstaltungsorten wie dem Prager Frühlingsfestival, dem Lincoln Centre und der Carnegie Hall in New York, dem Auditorio Nacional Madrid, dem Mozarteum Salzburg, dem Théâtre des Châtelet in Paris, dem Konzerthaus Berlin und vielen anderen. Er hat Dutzende neuer Stücke uraufgeführt, z. B. von Frederic Rzewski, Clarence Barlow, Maria De Alvear, Fred Frith und Gordon Mumma. Er ist einer der wenigen Pianisten weltweit, die das gesamte Opus Clavicembalisticum von Sorabji spielen. Neben seiner Tätigkeit als Solist bildet er ein Klavierduo mit dem legendären australischen Pianisten Geoffrey Douglas Madge und tritt im Duo mit dem Cellisten Arne Deforce und der Sängerin Salome Kammer auf. Seit 2001 unterrichtet er Klavier am Konservatorium von Gent, University of Ghent College.
Details
- Datum:
- 5. Juli 2024
- Zeit:
-
19:00 -20:30
- Veranstaltungskategorie:
- Konzert
- Veranstaltung-Tags:
- Approximating Pi, Clarence Barlow, Daan Vandewalle, Fixed Media, Julia Puls, Maximilian Adler
Veranstaltungsort
- ligeti zentrum, 10. Stock
-
Veritaskai 1
Hamburg, 21079 Germany Google Karte anzeigen - Veranstaltungsort-Website anzeigen